Łożyska toczne są często psującymi się elementami maszyn i podlegają relatywnie częstym wymianom, niektóre z nich psują się cyklicznie, aczkolwiek nie jest to regułą. Uszkodzenie łożyska może być spowodowane nadmierną eksploatacją, wadą materiałową, dokładnością wykonania czy przypadkowym zabrudzeniem. Najczęściej łożysko psuje się w sposób stopniowy, jakaś z przyczyn inicjuje przyspieszone zużycie aż do momentu zupełnego zniszczenia. Temat wczesnego wykrycia uszkodzenia łożyska jest dobrze opracowany, na rynku istnieją zaawansowane urządzenia pozwalające na diagnostykę tychże części maszyn.

Popularną metodą oceny zużycia łożyska jest analiza drgań przez nie emitowanych. Sama ich amplituda, czy kolokwialnie mówiąc głośność pracy może być organoleptycznie oceniona. Inaczej mówiąc kiedy łożysko się uszkodzi zaczyna je być “mocniej” słychać. Nie zawsze jednak jest możliwe aby je usłyszeć. W miejscach rzadko odwiedzanych, pracujących autonomicznie oraz tam gdzie hałas i poziom innych dźwięków otoczenia jest zbyt duży, dźwięk samego łożysko może zostać zagłuszony.

Istnieje dobrze opracowana teoria na temat tego jaki typ uszkodzenia powoduje zwiększoną emisję drgań. Rozróżniamy kilka podstawowych typów uszkodzeń; uszkodzenie bieżni pierścienia zewnętrznego lub wewnętrznego, uszkodzenie elementu tocznego jak i również tzw. koszyka i uszczelniacza. Każde z tych typów wg teorii generować będzie charakterystyczne drgania. Do oceny charakteru drgań z pomocą przychodzi nam transformata Fouriera (Rys. 1) z której wykresu możemy odczytać jakie częstotliwości są dominujące i według opracowanych wcześniej wzorów oszacować czy dane łożysko jest uszkodzone w konkretny sposób. Czynność ta jednak wymaga posiadania odpowiedniego sprzętu i wiedzy niezbędnej do wyciągnięcia takiego wniosku.

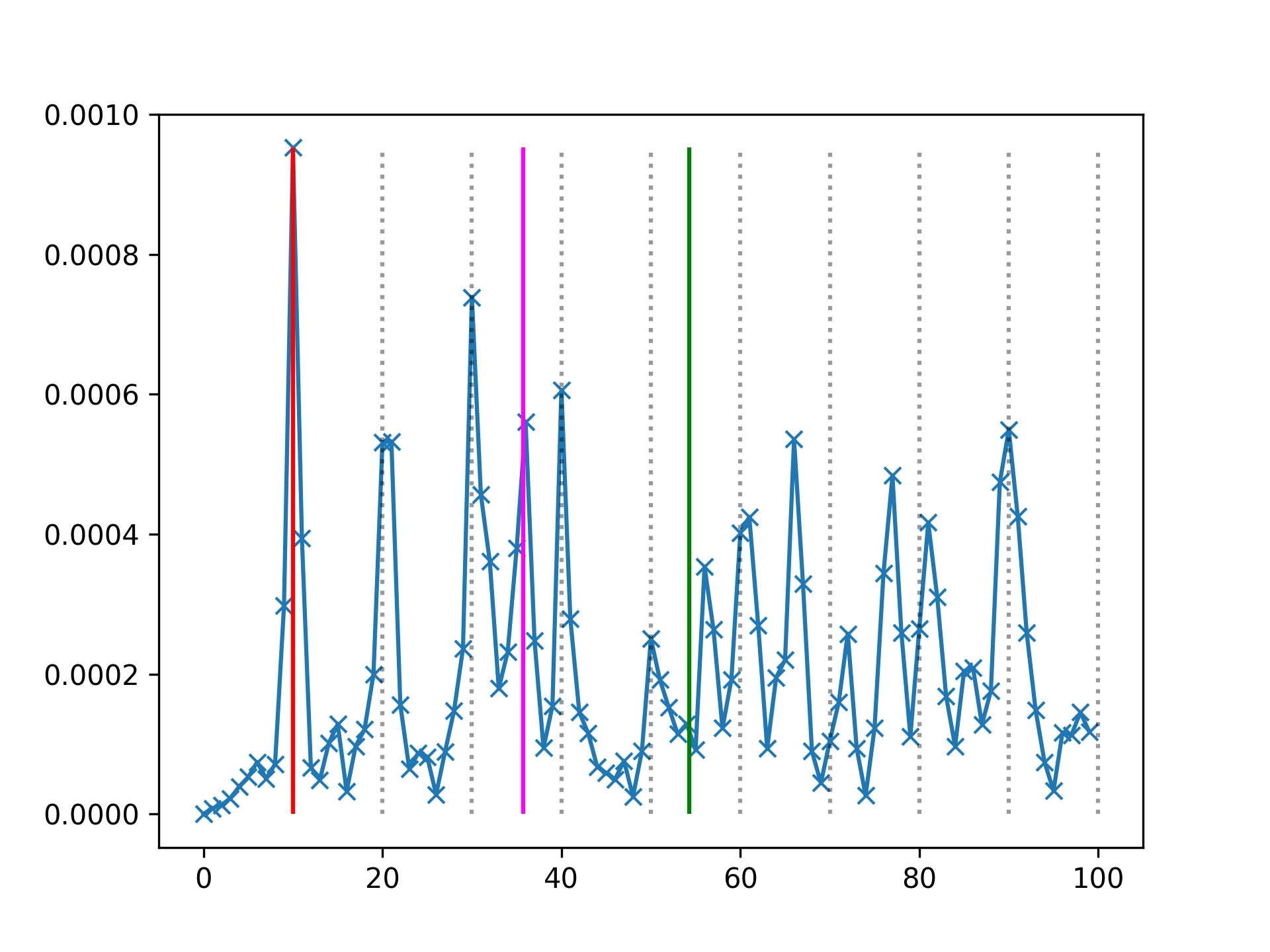
Sztuczna inteligencja będąca tak naprawdę pewnym rodzajem oprogramowania komputerowego które może przyjść nam z pomocą, wedle ogólnych zaleceń powinna być stosowana tam gdzie stworzenie oprogramowania byłoby kłopotliwe z uwagi na niejednoznaczność dostarczonych do analizy danych jak i zaszumienie sygnału czynnikami zewnętrznymi. Napisanie programu który w sposób analityczny wykrywa uszkodzenie przy użyciu instrukcji warunkowych mogłoby okazać się bardzo kłopotliwe. W takich właśnie przypadkach trafnym wyborem mogą okazać się algorytmy AI (Artificial Intelligence). Podejście takie nie jest jednak pozbawione wad, algorytmy AI, których zadaniem jest niejako zakwalifikowanie łożyska jako dobrze pracujące lub uszkodzone wymagają tzw nauki. Koniecznym jest ich wytrenowanie poprzez podanie czasem i sporej ilości danych i wskazanie który z sygnałów pochodzi z jakiego stanu. Przypadek łożysk jest dodatkowo kłopotliwy, gdyż częstotliwości cech charakterystycznych są zależne od konstrukcji łożyska tj. jego rozmiarów i ilości elementów tocznych.  Niepomijalnym jest również odpowiednie przygotowanie danych poprzez np filtrowanie i skalowanie, tak aby poniekąd pomóc modelowi w identyfikacji wspomnianych wyżej cech sygnału odpowiedzialnych za poszczególne typy uszkodzeń.

Z nieprzebranej zawartości zasobów internetu można ściągnąć nagrania jednego typu łożyska ER16K. Dane zostały opracowane na Kanadyjskim uniwersytecie w Ottawie przez Huan Huang, Natalie Baddour i opublikowane na łamach ELSEVIER jako artykuł “Bearing vibration data collected under time-varying rotational speed conditions” w 2018r. Zawierają one odczyty pracującego łożyska zarówno dla stanu nieuszkodzonego jak i poszczególnych typów uszkodzeń. Zarejestrowane informacje to: zmienna prędkość obrotowa łożyska i odczyty mierzonych wibracji w postaci przyspieszeń. Częstotliwość próbkowania wynosiła 200 kHz. Każdy stan łożyska został zarejestrowany dla kolejno: jednostajnie wzrastającej i malejącej prędkości jak i również dla wzrastającej a następnie malejącej i odwrotnie, po 3 różne próbki dla każdego schematu prędkości (Rys. 2).

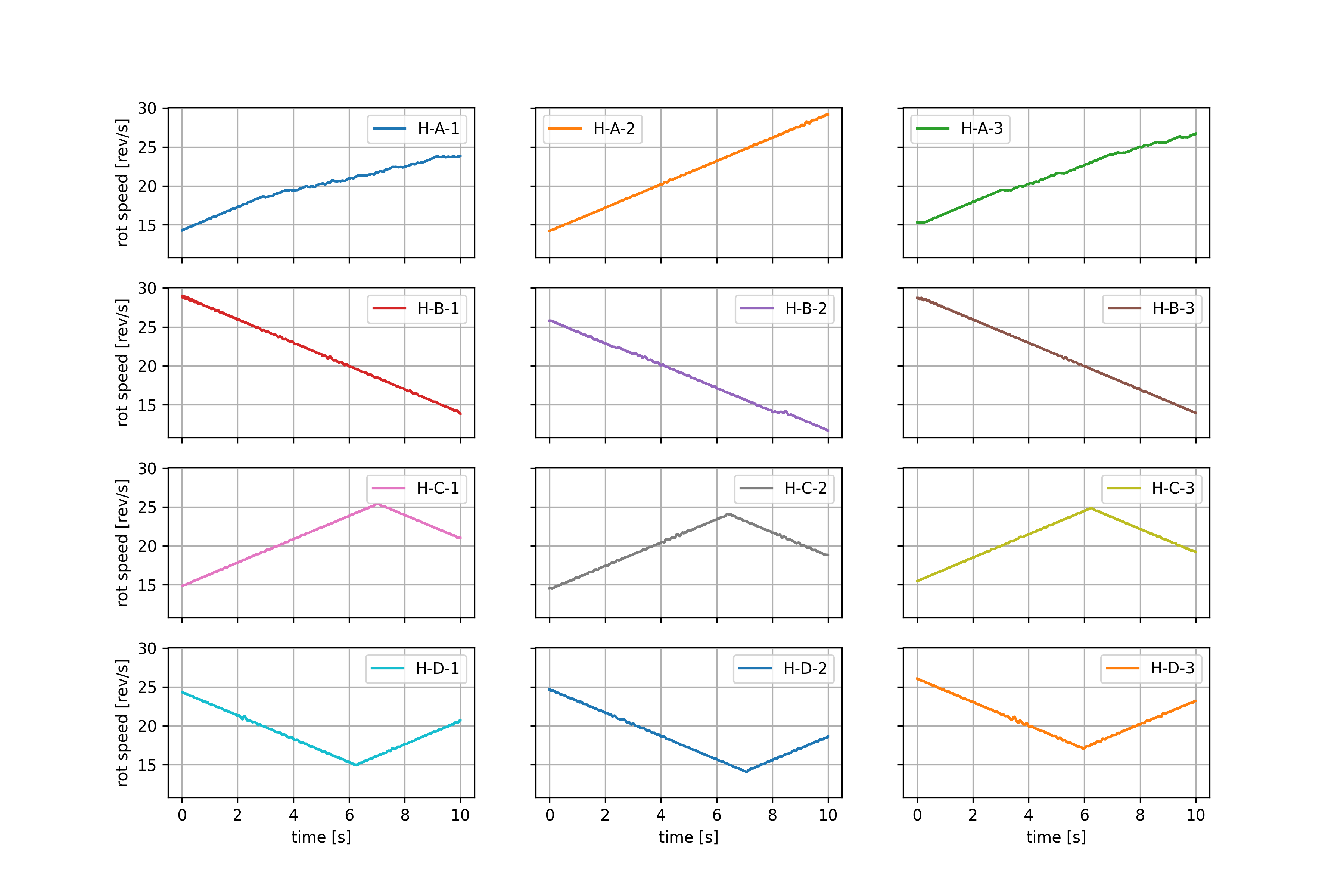
Do powyższego opracowania została przyjęta metoda oceny stanu łożyska na podstawie analizy widma częstotliwości drgań (przyspieszenia) z wykorzystaniem transformaty Fouriera FFT. Obrabiany sygnał o długości 10 sekund zawierający 2’000’000 odczytów, który został podzielony na 20 równych półsekundowych części. Dla każdej z takich części została wyznaczona osobna transformata Foureira (Rys.3). Tak przygotowane dane zostały następnie poddane procesowi normalizacji częstotliwości.